How Do You Find The Focus Of A Parabola

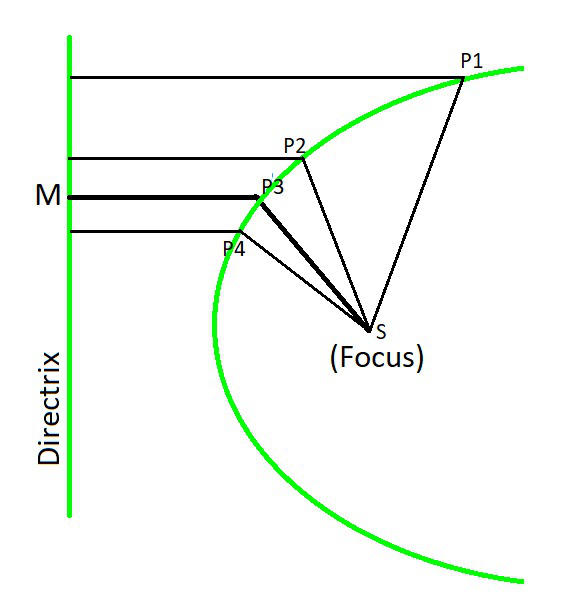
In mathematics, a parabola is the locus of a point that moves in a plane where its distance from a fixed point known equally the focus is ever equal to the distance from a fixed direct line known equally directrix in the same plane. Or in other words, a parabola is a plane curve that is well-nigh in U shape where every signal is equidistance from a fixed signal known as focus and the straight line known as directrix. Parabola has only i focus and the focus never lies on the directrix. As shown in the beneath diagram, where P_aneM = P₁S, P₂1000 = P_iiSouthward, P₃M = P₃South, and P_fourM = P_ivS.

Equation of the parabola from focus & directrix

At present we will acquire how to find the equation of the parabola from focus & directrix. Then, let S exist the focus, and the line ZZ' exist the directrix. Depict SK perpendicular from S on the directrix and bisect SK at V. Then,

VS = VK

The distance of V from the focus = Distance of Five from the directrix

5 lies on the parabola, So, SK = 2a.

So, VS = VK = a

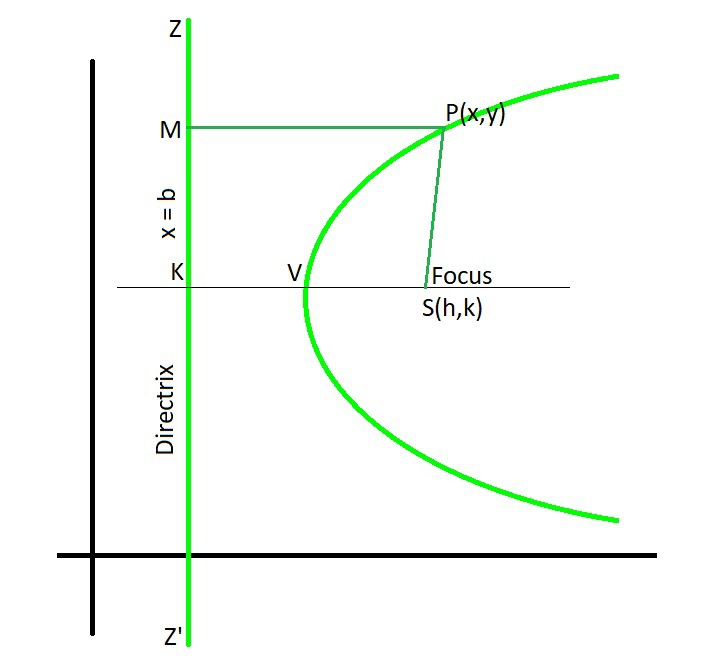
Let's accept 5 as vertex, VK is a line perpendicular to ZZ' and parallel to the x-centrality. And then, the coordinates of focus S are (h, chiliad) and the equation of the directrix ZZ' is x = b. PM is perpendicular to directrix x = b and point M volition exist (b, y)

Let united states of america considered a point P(x, y) on the parabola. Now, join SP and PM.

As we know that P lies on the parabola

So, SP = PM (Parabola definition)

SPⁱⁱ = PM^two

(10 – h)^two + (y – k)² = (x – b)² + (y – y)²

xⁱⁱ – 2hx + h² + (y-k)² = x² – 2bx + b²

Add together (2hx – b^two) both side, nosotros get

x^two – 2hx + h^two + 2hx – b² + (y-one thousand)^two = tenⁱⁱ – 2bx + b² + 2hx – b²

two(h – b)x = (y-m)² + hⁱⁱ – b^two

Divide equation by 2(h – b), we become

ten = $\frac{(y-k)^2}{2(h-b)} + \frac{(h-b)(h+b)}{2(h-b)}$

ten = $\mathbf{\frac{(y-k)^2}{2(h-b)} + \frac{(h+b)}{2}}$ ………………..(1)

Similarly when directrix y = b, we become

y = $\mathbf{\frac{(x-h)^2}{2(k-b)} + \frac{(k+b)}{2}}$ ………………..(2)

When 5 is origin, VS as x-axis of length a. Then, the coordinates of S volition be (a, 0), and directrix ZZ' is ten = -a.

h = a, k = 0 and b = -a

Using the equation (i), nosotros go

x = $\frac{(y-0)^2}{2(a-(-a))} + \frac{(a+(-a))}{2}$

x = $\frac{y^2}{4a}$

y² = 4ax

It is the standard equation of the parabola.

Notation: The parabola has two real foci situated on its axis one of which is the focus S and the other lies at infinity. The corresponding directrix is also at infinity.

Tracing of the parabola yⁱⁱ = 4ax, a>0

The given equation tin exist written as y = ± 2 $\sqrt{ax}$ , we observe the following points from the equation:

Symmetry: The given equation states that for every positive value of x, there are two equal and reverse value of y.
Region: The given equation states that for every negative value of x, the value of y is imaginary which means no role of the curve lies to left of the y-axis.
Origin: Origin is the point from where the curve passes through and the tangent at the origin is ten = 0 i.e., y-centrality.
Portion occupied: As x⇢∞, y⇢∞. Hence the curve extends to infinity to the correct of the axis of y.

Another standard forms of the parabola with focus and directrix

The simplest form of the parabola equation is when the vertex is at the origin and the axis of symmetry is forth with the x-axis or y-axis. Such types of parabola are:

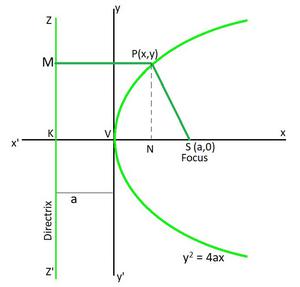
i. y² = 4ax

Hither,

Coordinates of vertex: (0, 0)
Coordinates of focus: (a, 0)
Equation of the directrix: x = -a
Equation of centrality: y = 0
Length of the latus rectum: 4a
Focal altitude of a betoken P(x, y): a + x

2. xⁱⁱ = 4ay

Here,

Coordinates of vertex: (0, 0)
Coordinates of focus: (-a, 0)
Equation of the directrix: x = a
Equation of axis: y = 0
Length of the latus rectum: 4a
Focal altitude of a point P(10, y): a – x

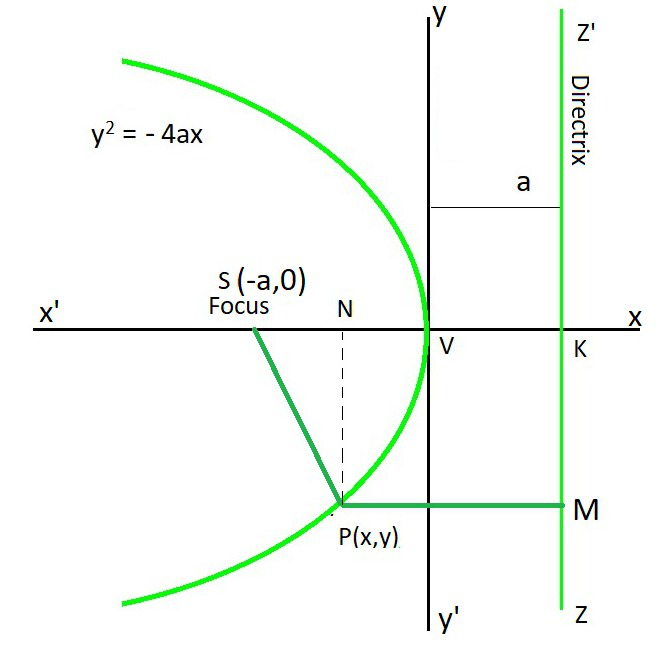
3. y² = – 4ay

Hither,

Coordinates of vertex: (0, 0)
Coordinates of focus: (0, a)
Equation of the directrix: y = -a
Equation of axis: 10 = 0
Length of the latus rectum: 4a
Focal distance of a point P(x, y): a + y

4. xⁱⁱ = – 4ay

Here,

Coordinates of vertex: (0, 0)
Coordinates of focus: (0, -a)
Equation of the directrix: y = a
Equation of axis: 10 = 0
Length of the latus rectum: 4a
Focal distance of a bespeak P(10, y): a – y

Sample Problems

Question 1. Find the equation of the parabola whose focus is (-4, two) and the directrix is x + y = three.

Solution:

Permit P (x, y) exist any signal on the parabola whose focus is (-4, ii) and the directrix x + y – three = 0.

Every bit nosotros already know that the altitude of a bespeak P from focus = altitude of a point P from directrix

So, √(x + iv)² + (y – 2)²= $|\frac{x+y-3}{\sqrt{1^2+1^2}}|$

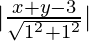
On squaring both side we get

(ten + 4)² + (y – two)²= $|\frac{x+y-3}{\sqrt{2}}|^2$

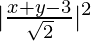
ii((xⁱⁱ + 16 + 8x) + (y²+ four – 4y)) = x^two + y² + ix +2xy – 6x – 6y

2(ten² + 20 + 8x + y²– 4y) = 10² + y² + 9 +2xy – 6x – 6y

2x^two + 40 + 16x + 2yⁱⁱ– 8y = x² + y² + 9 +2xy – 6x – 6y

ten² + yⁱⁱ + 2xy + 10x – 2y + 31 = 0

Question 2. Find the equation of the parabola whose focus is (-four, 0) and the directrix x + 6 = 0.

Solution:

Let P (x, y) be any betoken on the parabola whose focus is (-4, 0) and the directrix x + 6 = 0.

As we already know that the altitude of a point P from focus = distance of a point P from directrix

So, √(x + iv)² + (y )²= $|\frac{x+6}{\sqrt{1^2+1^2}}|$

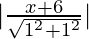
On squaring both side nosotros get

(x + 4)^two + (y)^two= $|\frac{x+6}{\sqrt{2}}|^2$

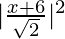
2x² + 32 + 16x + 2y²= 10² + 36 + 12x

x² + 2yⁱⁱ – 4 + 14x = 0

Question 3. Find the equation of the parabola with focus (iv, 0) and directrix ten = – 3.

Solution:

Since the focus (4, 0) lies on the x-axis, the 10-axis itself is the axis of the parabola.

Hence, the equation of the parabola is of the form either

y²= 4ax or y^two= – 4ax.

Since the directrix is x = – 3 and the focus is (iv, 0),

the parabola is to be of the form yⁱⁱ= 4ax with a = 4.

Hence, the required equation is

y² = iv(iv)ten

y² = 16x

Question iv. Find the equation of the parabola with vertex at (0, 0) and focus at (0, 4).

Solution:

Since the vertex is at (0, 0) and the focus is at (0, v) which lies on y-axis, the y-axis is the axis of the parabola.

Hence, the equation of the parabola is xⁱⁱ= 4ay.

Hence, we have xⁱⁱ = four(iv)y, i.e.,

x^two = 16y

Focus & directrix of a parabola from the equation

At present we volition learn how to find the focus & directrix of a parabola from the equation.

So, when the equation of a parabola is

y – k = a(10 – h)²

Here, the value of a = one/4C

So the focus is (h, g + C), the vertex is (h, m) and the directrix is y = k – C.

Sample Examples

Question i. yⁱⁱ = 8x

Solution:

The given parabola is of the form yⁱⁱ = 4ax, where

4a = 8

a = 2

The coordinates of the focus are (a,0), i.e. (2,0)

and, the equation of the directrix is

x = -a, i.eastward. x = -2

Question 2. y² – 8y – ten + 19 = 0

Solution:

By rearranging, we get

y² – 8y + 16 – 10 + 3 = 0

y² – 8y + 16 = x – 3

x = (y-4)² + iii

Comparison with eq(ane), we conclude

chiliad = four

2(h-b) = i ……………(I)

$\frac{(h+b)}{2}$ = 3 ……………(II)

Solving (I) and (II), we get

h = $\frac{13}{4}$ and b = $\frac{11}{4}$

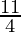
Hence, Focus is (h,g) = ( $\frac{13}{4}$ ,4)

and, directrix x = b = $\frac{11}{4}$

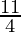
Question three. Find focus, directrix and vertex of the post-obit equation: y = x² – 2x + 3

Solution:

By rearranging, we get

y =10² – 2x + 4 – 1

y =(ten-1)ⁱⁱ + 2

Comparing with eq(four), we conclude

h = one

y_one = 2

two(k-b) = one ……………(I)

$\frac{(k+b)}{2}$ = 2 ……………(II)

Solving (I) and (2), we get

grand = $\frac{9}{4}$

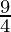
and b = $\frac{7}{4}$

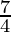
Hence, Focus is (h,k) = ( 1, $\frac{9}{4}$ ),

directrix y = b = $\frac{7}{4}$

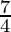
and, vertex (h, y₁) = (1,2)